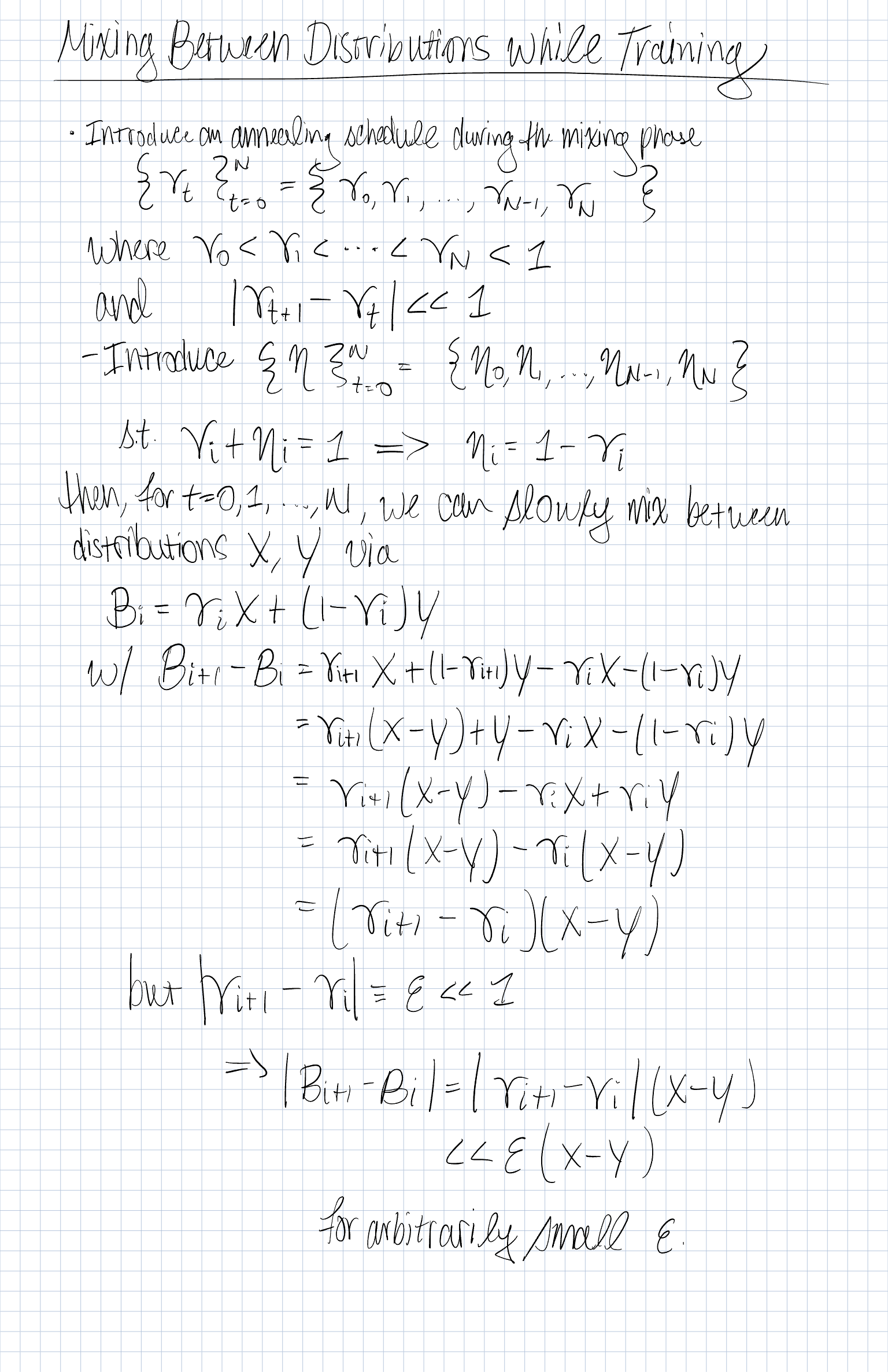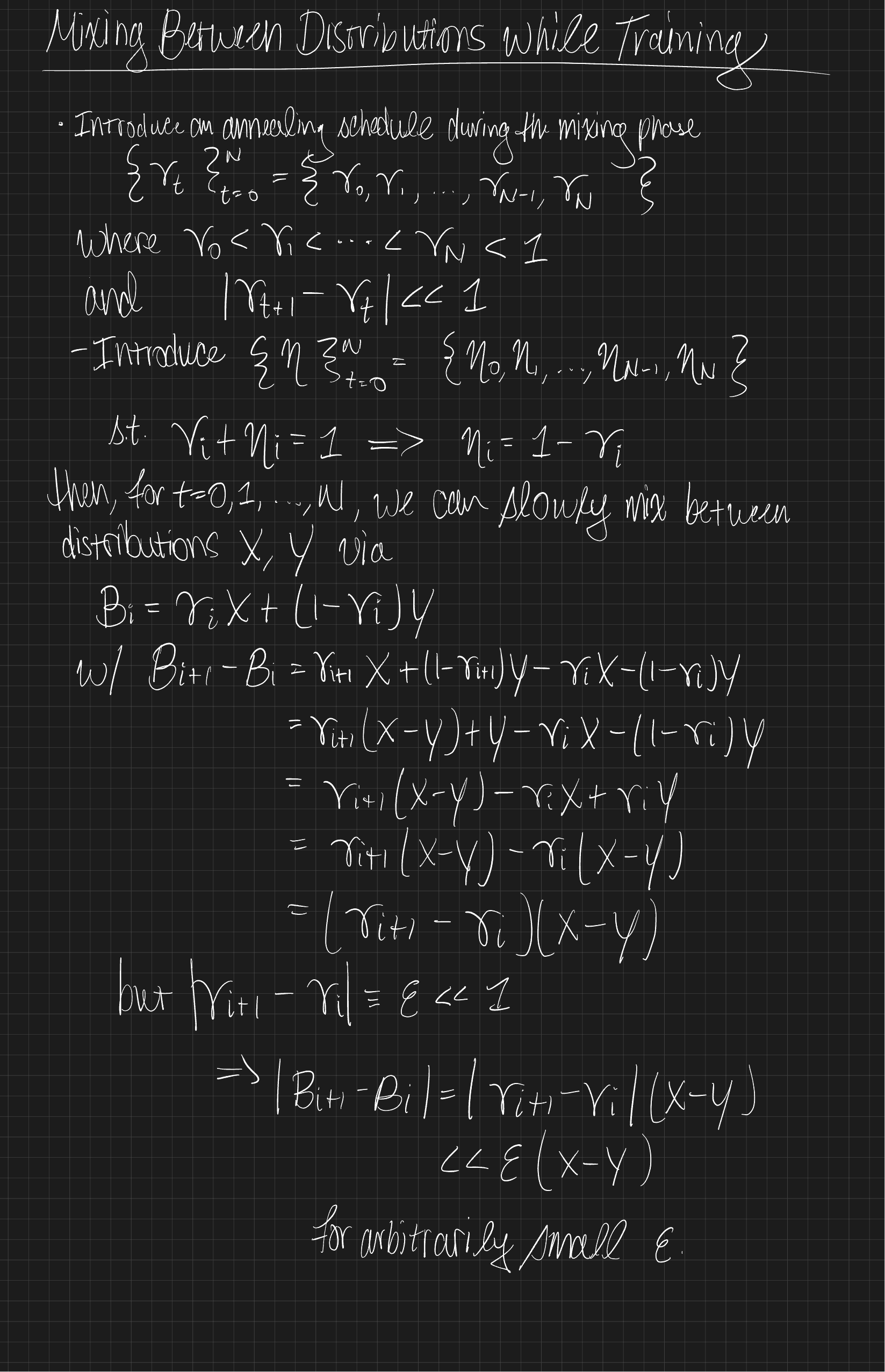🎨 Mixing Between Distributions While Training

A framework for smoothly interpolating between two distributions during training.

Author

Affiliation

Sam Foreman

ALCF

Motivation

When training on multiple data sources or domains, it is often desirable to smoothly interpolate between two distributions rather than switching abruptly. This ensures stable optimization and avoids sudden shifts in gradient statistics.

We can achieve this with an annealing schedule that gradually shifts probability mass from one distribution to another.

Mathematical Framework

We introduce an annealing schedule during the mixing phase:

$$\{\gamma_t\}_{t=0}^N = \{\gamma_0, \gamma_1, \ldots, \gamma_{N-1}, \gamma_N\}$$

where

$$\begin{aligned} 0 < \gamma_0 < \gamma_1 &< \cdots < \gamma_N < 1 \\ \quad |\gamma_{t+1} &- \gamma_t| \ll 1. \end{aligned}$$

We also define a complementary schedule:

$$\{\eta_t\}_{t=0}^N = \{\eta_0, \eta_1, \ldots, \eta_N\}, \quad \text{with } \gamma_i + \eta_i = 1 \implies \eta_i = 1 - \gamma_i.$$

Mixing Definition

For (t = 0, 1, , N), define the interpolated distribution

$$B_i = \gamma_i X + (1 - \gamma_i) Y,$$

where (X) and (Y) are two underlying distributions (or datasets, or losses).

Incremental Difference

The change between successive mixtures is:

$$\begin{aligned} B_{i+1} - B_i &= \gamma_{i+1} X + (1 - \gamma_{i+1}) Y - \left[ \gamma_i X + (1 - \gamma_i) Y \right] \\ &= (\gamma_{i+1} - \gamma_i)(X - Y). \end{aligned}$$

Thus,

$$|B_{i+1} - B_i| = |\gamma_{i+1} - \gamma_i| \, |X - Y|.$$

If we set $|\gamma_{i+1} - \gamma_i| = \varepsilon \ll 1$, then

$$|B_{i+1} - B_i| \leq \varepsilon \, |X - Y|,$$

meaning the transition between (X) and (Y) is arbitrarily smooth.

Interpretation

• This is a linear interpolation (convex combination) between two distributions.
  
• The annealing schedule ensures that the interpolation is smooth in small increments.
  
• Useful in:
  • Curriculum learning: start from an easier distribution and anneal to a harder one.
  • Domain adaptation: gradually shift from source domain (X) to target domain (Y).
  • Robust training: maintain a mixture for diversity and stability.

Implementation

Below is a simple Python implementation of such a schedule and a sampler that mixes between two datasets.

import math, random
from typing import List, Sequence, Any, Iterator, Tuple

def make_schedule(n_steps: int, start: float = 0.0, end: float = 1.0, kind: str = "linear") -> List[float]:
    """Generate an annealing schedule."""
    if kind == "linear":
        return [start + (end - start) * (t / (n_steps - 1)) for t in range(n_steps)]
    elif kind == "cosine":
        return [
            start + (end - start) * (1 - math.cos(math.pi * t / (n_steps - 1))) / 2
            for t in range(n_steps)
        ]
    else:
        raise ValueError(f"Unknown schedule kind: {kind}")

class MixtureSampler:
    """Probabilistic mixture of two datasets using gamma_t schedule."""
    def __init__(self, X: Sequence[Any], Y: Sequence[Any], schedule: Sequence[float]):
        self.X, self.Y = X, Y
        self.schedule = schedule
        self.rng = random.Random(0)

    def __iter__(self) -> Iterator[Tuple[int, Any]]:
        for t, gamma_t in enumerate(self.schedule):
            if self.rng.random() < gamma_t:
                yield t, self.X[self.rng.randrange(len(self.X))]
            else:
                yield t, self.Y[self.rng.randrange(len(self.Y))]

# Example usage
if __name__ == "__main__":
    X = [("X", i) for i in range(5)]
    Y = [("Y", i) for i in range(5)]
    sched = make_schedule(10, start=0.1, end=0.9, kind="cosine")
    mix = MixtureSampler(X, Y, sched)

    for t, ex in mix:
        print(f"t={t:02d}, gamma={sched[t]:.2f}, sample={ex}")

Original Notes

Figure 1: Original Notes